Shared Experience Actor-Critic for Multi-Agent Reinforcement Learning

Quick summary:

• General method for efficient MARL exploration by sharing experience amongst agents with decentralized policies.
• Allows for agents to learn distinct behaviour and enables the group of agents develop a better coordination.
• Agents learning at different rates might lead to sub-optimal policies.

Multi-Agent Reinforcement Learning (MARL) #

• Sparse reward example: 0 almost always except when the agent reaches the goal it gets +1.
• MARL needs to explore the environment’s dynamics + joint action space between agents. It’s very hard because other agents are non-stationary and even harder when the reward is sparse.
• Litterature:
  • Centralized training with decentralized execution (CTDE)
    • Training: learner has access to all agents’ transitions to learn policies that can be locally-executable (distributed).
    • MADDPG was unable to learn a good policy in a sparse-reward scenario.
  • Agents Teaching Agents
  • Learning from Demonstrations (from humans or other agents)
  • Distributed RL
    • A3C, IMPALA, SEED RL.
    • Several identical agents that are used to collect experience data for a single learner. Parameters of other agents are updated each N episodes with an off-policy correction.
  • Population-play
    • Train a population of diverse agents.
    • Explorations benefits since different agents affecting each other’s trajectory.
    • Costly in computational resources.

Preliminaries #

• Markov Games (POMDP): \((N, S, \{O^i\}, \{A^i\}, P, \{R^i\}\))
  • Agents: \(i \in N = {1, …, N}\)
  • \(O^i\) observation perceived by agent \(i\).
  • \(P: S \times A \rightarrow \Delta (S)\) gives transition distribution for the next states over the joint states and actions of all agents.
  • \(R^i: S \times A \times S \rightarrow \mathbb{R}\) gives a reward personalized for agent \(i\) (agents can learn collectively with different reward)
  • Objective of each agent: maximise \(G^i = \sum_{t=0}^{T} \gamma^t r^i_t\)
  • Assume: \(A = A^1 = … = A^N\) and \(O = O^1 = … = O^N\)
• PG and Actor-Critic
  • Classic policy loss: $$L(\phi_i) = -\log \pi(a^i_t | o^i_t; \phi_i) (r^i_t + \gamma V(o^i_{t+1}; \theta_i) - V(o^i_t; \theta_i))$$
  • Classic value loss: $$L(\theta_i) = || V(o^i_t; \theta_i) - y_i ||^2 \text{ with } y_i = r_t^i + \gamma V(o_{t+1}^i; \theta_i)$$

Shared Experience Actor-Critic #

Method #

• Assumption: local policy gradients provide useful learning directions for all agents. Gradients come from the policy, so the reward isn’t involved => agents can have different rewards.
• Need to add importance sampling since updates can come from other policies. Using the following, each agent is trained on both on-policy data while also using the off-policy data collected by all other agents at each training step.
  • New Policy loss that accounts for updates from other agents (k). Scroll: $$L(\phi_i) = -\log \pi(a^i_t | o^i_t; \phi_i) (r^i_t + \gamma V(o^i_{t+1}; \theta_i) - V(o^i_t; \theta_i)) - \lambda \sum_{k \ne i} \frac{\pi(a^k_t | o^k_t;\phi_i)}{\pi(a^k_t | o^k_t;\phi_k)} \log \pi(a^k_t | o^k_t; \phi_i) (r^k_t + \gamma V(o^k_{t+1}; \theta_i) - V(o^k_t; \theta_i))$$
  • New Value loss that accounts for updates from other agents (k). Scroll: $$L(\theta_i) = || V(o^i_t; \theta_i) - y_i ||^2 + \lambda \sum_{k \ne i}\frac{\pi(a_t^k | o_t^k;\phi_i)}{\pi(a_t^k | o_t^k; \phi_k)} || V(o^i_t; \theta_i) - y_k^i ||^2 \text{ with } y_i^k = r_t^k + \gamma V(o_{t+1}^k; \theta_i)$$
  • \(\lambda\): weight of experience from other agents (doesn’t really matter, use \(\lambda = 1\))

Experiments #

Environments #

• Predator Prey: If at least 2 predators are close to the prey they receive a reward of 1, if they leave the map they receive negative reward, otherwise the reward is zero.
• SMAC (SC2 Multi-Agent Challenge): variant that the agent controls several marines with a reward of 1 upon winning and a reward of -1 if facing defeat.
• Label-Based Foraging: rewards from fraction of items collected per episode compared to other agents.
• Multi-Robot Warehouse: POMDP (limited view), very sparse reward signal only seen upon making a successful delivery.

Baseline algorithms #

• Independent Actor-Critic (IAC): independent policies with independent learning.
• Shared Network Actor-Critic (SNAC): single policy that is updated online by each agent, each agent executes a copy of that policy.

Algorithm details #

• 5-step returns with 4 environments were sampled in batches to the optimiser.
• Entropy regularization term (relative to agent \(i\)) added to each agent \(i\) loss

Results #

• PP only SEAC learns successfully.
• SMAC means are close to 0.0. The agents learned to ran away from the enemy instead of winning the battle. SOTA methods designed for this environment don’t even solve this sparsely rewarded task.
• LBF & RWARE same for easy variant, but as rewards become sparser, SEAC improves a lot compared to baselines and tends to converge faster.

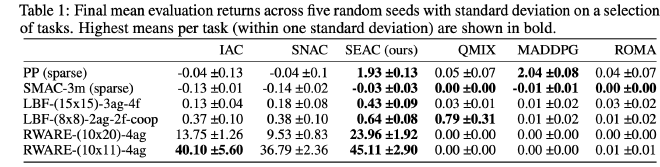
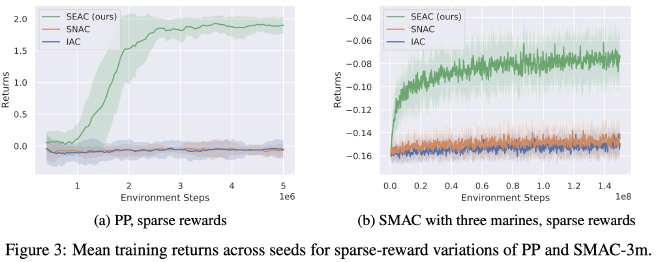
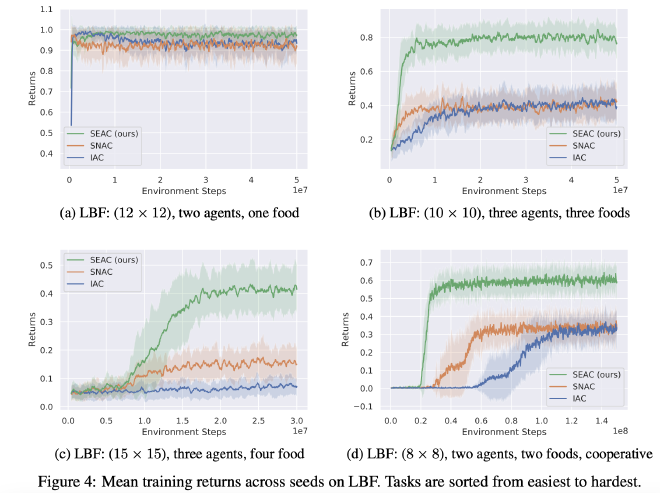
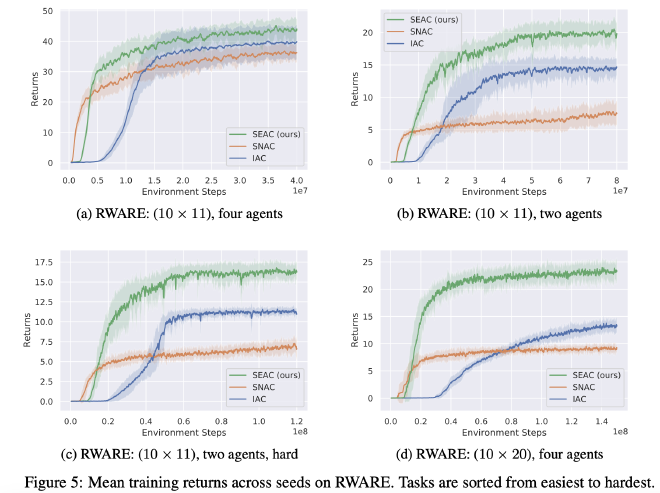
• Different policies learned:
  • Agents learn similar but slightly different policies (importance weights sampled are centred around 1)
  • Agents have different policies because of the random initialization of the networks and because of the agent-centred entropy factor.
• Issues:
  • Agents learning at different rate impede each other’s ability to learn, leading to sub-optimal policies.
    • Agents with slightly less successful exploration have a harder time learning a rewarding policy when the task they need to perform is constantly done by others.
    • In SC2, a single agent can’t win if other agents aren’t helping the fight. The agent would learn to avoid the fight, which is not optimal.