Quick summary:

• Solving complex tasks without access to the reward function.
• Little human oversight to enable the agent to learn behaviors that are complex and hard to define in a reward function.
• Agents can learn from non-experts of the environment.

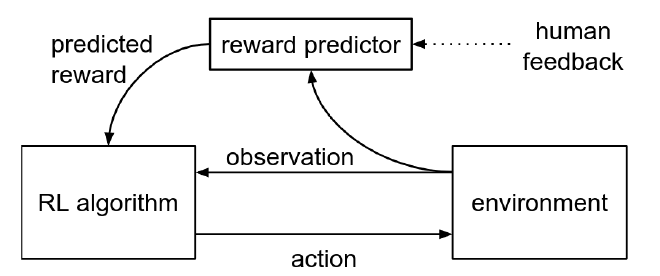
Method #

Goal setting: #

• Environment receives the action from the agent and only share the new observation \(o_t\) to the agent.
• Reward is not provided by the environment, but learned from a human overseer’s preferences over a trajectory \(\sigma = {(o_0, a_0), (o_1, a_1), …, (o_k, a_k)}\).

Proposed method: #

• 2 Neural Networks: the policy \(\pi : O \rightarrow A\) and the reward function estimate \(\hat{r} : O \times A \rightarrow \mathbb{R}\)
• Update the networks by 3 processes (running async):
  • \(\pi\) interacts with the environment to produce a set of trajectories \({\tau^1, …, \tau^i}\) and \(\pi\) is updated using traditional RL to maximise rewards from estimate \(\hat{r}\).
    • \(\hat{r}\) is non-stationnary: prefer algorithms that are more resistant to such rewards (e.g. TRPO, PPO).
    • \(\hat{r}\) normalized to zero mean and constant std.
  • Select pairs of segments (\(o^1, o^2\)) from generated trajectories above and send them to a human for comparison.
    • Human chooses: the most preferable one, equal or unable to compare (in which case the comparison is ignored).
    • Preferences are recorded in a db \(D\) of triples \((\sigma^1, \sigma^2, \mu)\), where \(\mu\) is the distribution of the preference over segments (i.e. if one is prefered, \(\mu\) puts all its mass on the preference, if segments are equal, then the distribution is uniform).
    • Selecting queries: make estimations+preferences using models from the ensemble on a large number of trajectories/segments. Select queries for which the segments produce a higher variance across ensemble models.
      • It may decrease performance!! We would instead want to query based on expected value information of the query (e.g. like highest TD-error for PER?).
  • Fit the parameters of \(\hat{r}\) via supervised learning on the comparisons collected so far from the humans.
    • \(\hat{r}\) can be interpreted as a preference-predictor (turning the estimated reward for both segments summed over the duration of the clip into density estimation of \(\mu\) from above):
      • \(\hat{P}[\sigma^1 \succ \sigma^2] = \frac{\exp \sum \hat{r}(o_t^1, a_t^1)}{\exp \sum \hat{r}(o_t^1, a_t^1) + \exp \sum \hat{r}(o_t^2, a_t^2)}\)
      • Which is basically: \(\frac{\text{Estimated rewards from segment 1}}{\text{Total estimated rewards for both segments}}\)
    • We optimize \(\hat{r}\) by minimizing the CE (\(\mu(x)\) is the human preference):
      • \(\text{loss}(\hat{r}) = - \sum_{(\sigma^1, \sigma^2, \mu)\in D} \mu (1) log\hat{P}[\sigma^1 \succ \sigma^2] + \mu (2) log \hat{P}[\sigma^2 \succ \sigma^1]\)
    • Using ensemble of predictors each trained on samples from \(D\) with replacement. Estimate is the result of independent normalization and average.
    • Regularization L2 and dropout sometimes used + validation samples.
    • Softmax is ajusted to account for a fixed 10% random error from human input (i.e. it’s like if 10% of the time the human chose a random action uniformly).

Results #

Unobserved reward (benchmark on scarcer rewards) #

1. Learning directly from human feedback on which trajectory is better. Using as few queries as possible.
2. Learn using a synthetic oracle which gives preferences over trajectories based on the reward in the underlying task (only provide the preference to the agent, not the actual reward).
3. Compare with baseline RL learning using the full/real reward function.

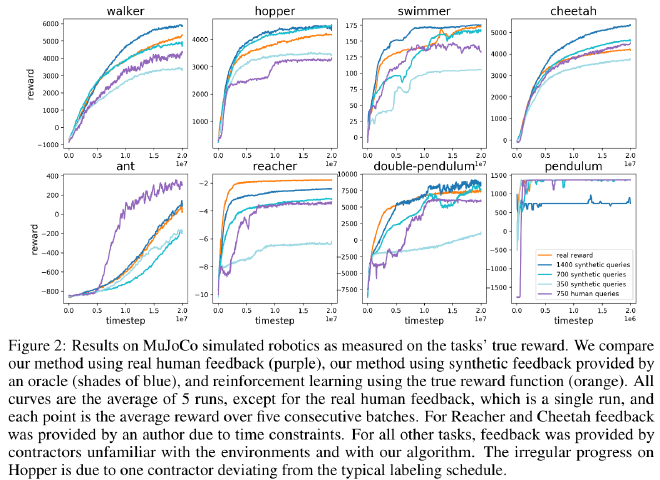
Simulated Robotics #

• Surprisingly, 1400 synthetic labels perform slightly better than if it was simply given the true reward (learned reward is better shaped?).
• Real human feedback is typically slightly less effective than the synthetic feedback (from half as efficient to equivalent in efficiency depending on the tasks).

  

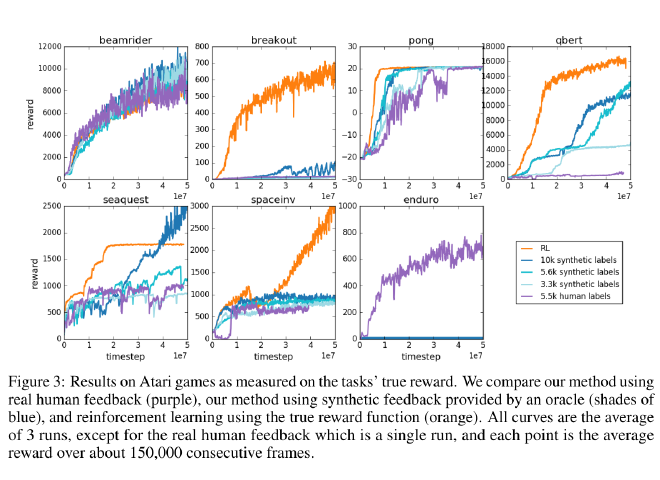
Atari #

• Real human feedback performs similar or worse than synthetic feedback (even sometimes similar to synthetic feedback with 40% less labels).
• Fails on Enduro since it’s hard to successfully pass other cars with random exploration. Humans tend to favor movements that allow to pass another car, thus performing better.

  

Novel behaviors #

No true rewards are defined for those goals:

1. The Hopper robot can perform multiple backflips.
2. Half-Cheetah can move forward whilst doing a handstand.
3. In Enduro, the agent stays almost exactly even with other moving cars, but gets confused with changes in background.

Ablation study #

1. Random queries: pick queries uniformly rather than prioritizing queries for which there’s a disagreement.
2. No ensemble: only one predictor and choose queries at random since there can’t be disagreements.
3. No online queries: train on offline training data (gathered at the beginning of training)
   • Poor performance. In general, human feedback needs to be intertwined with learning instead of provided statically. Otherwise, the predictor only captures part of the true reward which leads to bizarre behavior.
4. No regularization: use only dropout.
5. No segments: trajectory segments of length 1 for robotics tasks.
6. Target: oracle provides true total reward over a trajectory segment and we fit \(\hat{r}\) to these total rewards using MSE instead of fitting it using comparisons.
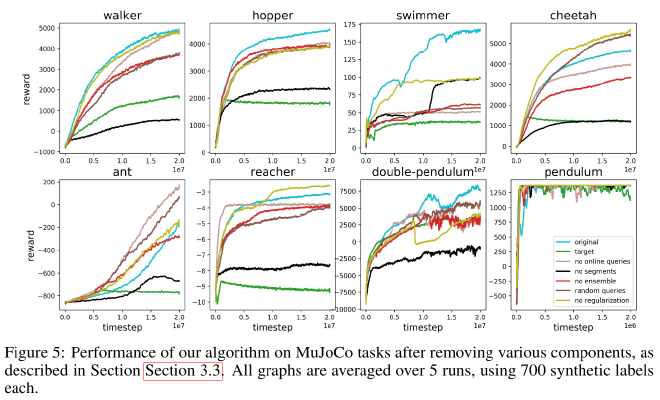
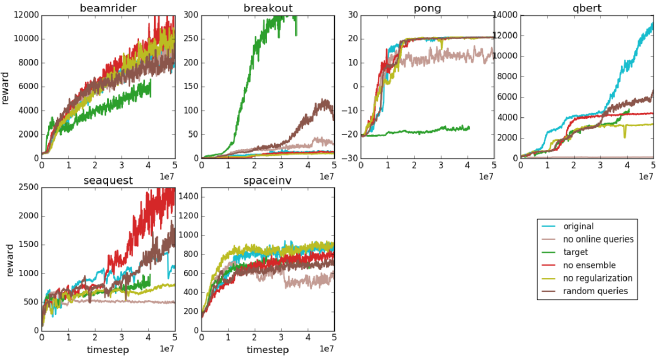
   • Results show that fitting rewards using comparisons provides almost always better results. (Always except for breakout)